Understanding Parsing using Examples

Understanding Parsing using Examples

In every example, we introduce a new start symbol (S’), and define a new production from this new start symbol to the original start symbol of the grammar.
Consider the following grammar (putting an explicit end-marker $ at the end of the first production):

(1) S’ → S$
(2) S → Sa
(3) S → b

For this example, the NFA for the stack can be shown as follows:

After doing ε-closure, the resulting DFA is as follows:

 

The states of DFA are also called “Canonical Collection of Items”. Using the above notation, the ACTION-GOTO table can be shown as follows:

Notice that there are two entries for state 2 on input ‘a’. So, this cannot be LR(0) grammar. So, the next enhancement is to look into the FOLLOW set of S’

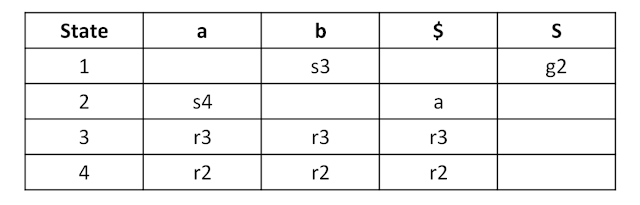
(which is {$}) and it is different from the shift symbol, this shift-reduce conflict can be resolved easily by reducing on input if it belongs to the FOLLOW set for
S’. This enhancement to parsing is called SLR(1) parsing. The correspondingtable can be written as follows:

Since there is no duplicate entry in the ACTION-GOTO table, this grammar is an SLR(1) grammar.Now, let’s look into progressive parsing of input string baa$.

First, let’s consider the case when the stack only contains the grammar symbols. The DFA at every step (shown in each entry of the following table) would
start from the bottom of the stack (identified with a ‘$’).

For the DFA to process from the bottom of the stack at every step is quite wasteful. So, it makes sense to save the grammar symbol along with the current

state into the stack. With this change, each stack entry (i..e, the LHS of |) is a pair of grammar symbol and state.

One step further than SLR(1) parsing is LR(1) parsing where the look-ahead is built into each item in the DFA. A slightly less powerful than LR(1), but more

space-optimized than LR(1) is LALR(1), which essentially combines the redundant states of LR(1) DFA into one state.